Renumitul nostru brutar a avut azi noapte un vis tare ciudat: acesta trăia într-un univers paralel în care nu omul îl mănâncă pe blat ci blatul îl mănâncă pe om… (eh, poate nu chiar atât de paralel). Astfel, brutarul nostru a fost atacat de blatul pe care tocmai îl pregătise (pentru prăjituri, evident) și a încercat să scape. Acesta a ieșit din brutărie și a ajuns în fața unui câmp de formă dreptunghiulară, cu dimensiunile cunoscute, ce poate fi împărțit în celule elementare cu latura de o unitate (exact ca o matrice!). Acesta poate intra pe câmp prin orice celulă a primei linii și trebuie să ajungă în orice celulă a ultimei linii (blatul se va întări până va ajunge acolo). Unele celule îi sunt inaccesibile din cauza diverselor obstacole (pietre, pomi, gropi,etc.)
Brutarul nostru se poate deplasa în 6 moduri:
- Din căsuța curentă în cele adiacente (
Nord,Vest,Sud,Est) - Două mișcări speciale ce pot varia.
Mutările speciale vor fi citite din fișier și o mutare se va codifica astfel: xA yB, unde x și y sunt numere naturale nenule iar A și B sunt două caractere ce codifică direcția (A poate fi 'N' sau 'S' de la Nord respectiv Sud iar B poate fi ‘E’ sau ‘V’ de la Est respectiv Vest)
Ex. 5N 2V codifică mutarea 5 poziții spre Nord și 2 poziții spre Vest. (din poziția (x,y) ajunge în poziția (x-5, y-2))
O mutare specială se poate face dacă celula destinație nu este ocupată de un obstacol și dacă nu implică ieșirea brutarului din matrice.
Cerința
Brutarul vă roagă să îi specificați un traseu cu număr minim de celule parcurse, ce pornește de pe prima linie și se termină pe ultima linie, pentru a nu fi blătuit (mâncat de blat).
Date de intrare
Pe prima linie a fișierului brutar.in se vor afla două numere naturale separate prin spațiu: N și M reprezentând numărul de linii și numărul de coloane ale câmpului. Urmează N linii a câte M caractere ‘X’ și ‘O’ unde ‘X' reprezintă obstacol iar ‘O’ reprezintă zonă liberă.
Ultimele două linii reprezintă codificarea celor două mutări speciale, câte o mutare pe o linie.
Date de ieșire
Fișierul brutar.out va conține, pe prima linie, numărul T de celule al unui traseu de lungime minimă. Următoarele T linii vor conține descrierea traseului, câte o celulă pe o linie, prin coordonatele ei, în ordinea în care au fost parcurse.
Restricții și precizări
1 ≤ N, M ≤ 1.0001 ≤ x ≤ N1 ≤ y ≤ M- Se garantează că mereu va există cel puțin un drum care pornește de pe prima linie și ajunge pe ultima linie a matricei.
- Dacă există mai multe soluții cu număr minim de pași, se poate afișa oricare dintre acestea.
Exemplu
brutar.in
14 10 XXXXXXOXXX OXOOOXOOOO OOXXOOXOXO OXOOOOXXXX OOOOXXOXOX OXOXOXXOOO XOXOOOOXOO OXXXOXOOOX XOOXOXOXOO OXOXOXOXOO OOOOXXOOXO XOOOXOXOOX OXOOOOOOOO XOXXXOXXXX 2S 1V 2S 1E
brutar.out
9 1 7 3 6 5 7 7 6 9 5 10 5 12 4 12 3 14 2
Explicație
Drumul este colorat în galben:
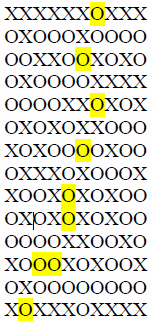
Cum e corect?
cout < "As la info";
cout << "As la info";
cout >> "As la info";
Felicitări! Poți mai mult?
Avem sute de probleme pentru tine, fiecare cu explicații ușor de înțeles.
Greșit, dar nu-i bai!
Antrenează-te cu sutele de probleme pe care ți le-am pregătit. Îți explicăm fiecare problemă în parte.
Rezolvare
Iată rezolvarea de 100 de puncte pentru problema Brutar:
// implementare: Cristi Dospra
// punctaj: 100p
// complexitate: O(N * M)
#include <fstream>
#include <algorithm>
#include <queue>
#include <vector>
using namespace std;
#define Nmax 1002
#define inf 0x3f3f3f3f
ifstream fin ( "brutar.in" );
ofstream fout ( "brutar.out" );
int N, M;
char v[Nmax][Nmax];
int Dist[Nmax][Nmax];
pair < int, int > Pred[Nmax][Nmax];
vector < pair < int, int > > Coords;
queue < pair < int, int > > Q;
bool Valid ( int x, int y ){
if ( x > 0 && x <= N && y > 0 && y <= M && v[x][y] != 'X' )
return 1;
return 0;
}
void Lee(){
for ( int i = 1; i <= M; ++i ){
if ( v[1][i] == 'O' ){
Q.push( make_pair( 1, i ) );
Dist[1][i] = 1;
}
}
while ( !Q.empty() ){
int x = Q.front().first;
int y = Q.front().second;
Q.pop();
vector < pair < int, int > > :: iterator it;
for ( it = Coords.begin(); it != Coords.end(); ++it ){
int xx = x + it->first;
int yy = y + it->second;
if ( Valid(xx,yy) && Dist[xx][yy] > Dist[x][y] + 1 ){
Q.push( make_pair(xx,yy) );
Dist[xx][yy] = Dist[x][y] + 1;
Pred[xx][yy] = make_pair( x, y );
}
}
}
}
void Remake ( int x, int y ){
if ( !x || !y )
return;
Remake( Pred[x][y].first, Pred[x][y].second );
fout << x << " " << y << "\n";
}
void Read(){
int x, y;
char a, b;
fin >> N >> M;
for ( int i = 1; i <= N; ++i ){
fin >> ( v[i] + 1 );
for ( int j = 1; j <= M; ++j ){
Dist[i][j] = inf;
}
}
Coords.push_back ( make_pair( -1, 0 ) );
Coords.push_back ( make_pair( 0, 1 ) );
Coords.push_back ( make_pair( 1, 0 ) );
Coords.push_back ( make_pair( 0, -1 ) );
for ( int i = 1; i <= 2; ++i ){
fin >> x >> a >> y >> b;
if ( a == 'N' )
x = -x;
if ( b == 'V' )
y = -y;
Coords.push_back( make_pair( x, y ) );
}
}
void Write(){
int Best = inf;
pair < int, int > Sol;
for ( int i = 1; i <= M; ++i ){
if ( Dist[N][i] < Best ){
Best = Dist[N][i];
Sol = make_pair( N, i );
}
}
fout << Best << "\n";
Remake( Sol.first, Sol.second );
}
int main(){
Read();
Lee();
Write();
return 0;
}
Atenție
Enunțurile afișate pe această pagină aparțin exclusiv site-ului PbInfo. Astfel, pentru ștergerea conținutului, puteți să ne contactați la adresa  .
.
Rezolvarea problemei #1761 Brutar
Pe această pagină găsești rezolvarea de 100 de puncte pentru problema #1761 Brutar de pe PbInfo.ro. Atenție: nu încurajăm copiatul codului! Totuși, credem cu tărie că analizarea unei soluții corecte este o metodă foarte ușoară de a învăța informatică, astfel că oferim sursele pentru peste 1500 de probleme de pe platforma PbInfo.ro.
Pentru rezolvări PbInfo de la peste 1500 de probleme, vă invităm să intrați pe site-ul nostru!