Magazinele IKEA au spre vânzare o categorie aparte de covoare, MORUM, pentru uz intern sau extern, rezistente la ploaie, soare, zăpadă şi noroi. Producătorul poate construi covoare MORUM clasice, dar poate construi și modele la alegerea clientului. Sunt trei modele puse la dispoziție de producători, generate în mai multe etape ale procesului de fabricație. Un covor se generează în mai multe etape, la fiecare etapă se decupează covorul conform desenelor de mai jos.
De exemplu, dacă covorul are formă de triunghi, în prima etapă se decupează un triunghi reprezentat în desen prin zona albă. În a doua etapă, din fiecare zonă triunghiulară neagră se va decupa folosind același procedeu ca la prima etapă un alt triunghi.

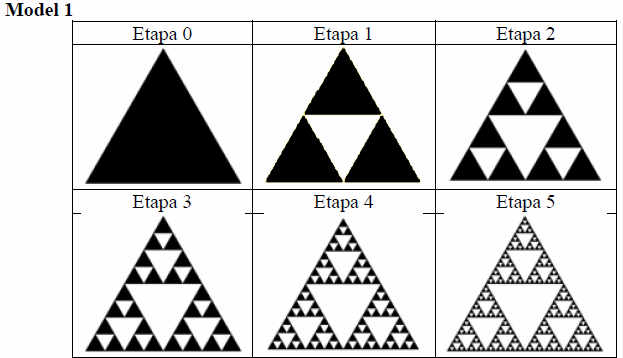
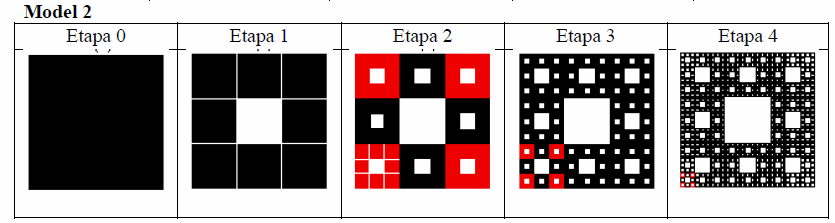
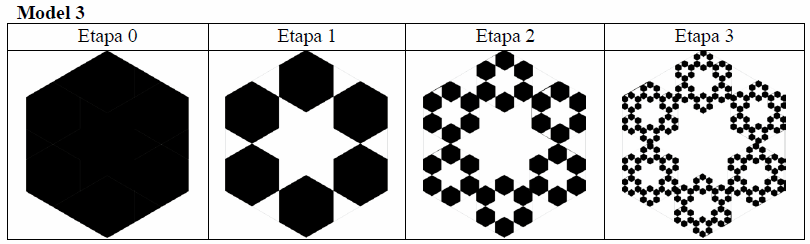
Deoarece, în procesul de dantelare, covoarele vor deveni din ce în ce mai fragile, producătorul solicită fiecărui cumpărător procentul din suprafața inițială care poate fi îndepărtat.

Cerința

Cunoscând latura l a covorului, modelul m ales, procentul p din suprafața inițială a covorului care poate fi decupat, determinați gradul de dantelare al covorului (etapa până la care se poate proceda la modelare), precum și lungimea conturului și suprafața covorului după decupare (perimetrul și aria se vor afișa fiecare prin câte o fracție).

Date de intrare

Fișierul morum.in conține pe prima linie, separate prin spațiu, valorile l, m și p.

Date de ieșire

Fișierul morum.out va conține pe prima linie gradul de dantelare, iar pe a doua linie un număr natural reprezentând numărătorul fracției ce reprezintă suprafața conturului, iar pe a treia linie numitorul fracției ce reprezintă suprafața suprafata conturului. Pe linia patru se afișează un număr natural ce reprezintă numărătorul fracției ce reține lungimea covorului, iar pe a cincea linie numitorul acesteia.

Restricții și precizări

latura covorului este un număr natural 𝑙≤1000000000;
procentul p este un număr natural cuprins între 1 și 99;
toate poligoanele inițiale și cele obținute prin decupare sunt regulate;
gradul de dantelare este un număr natural, reprezentând etapa la care se oprește procesul de decupare;
în calculele se va considera că √3=1.73=\(\frac{173}{100}\);
lungimea conturului şi aria vor fi reprezentate prin fracții; fracţiile nu sunt unice.
în urma dantelării materialul nu se destramă și formele din ce în ce mai mici care rămân vor rămâne prinse de restul covorului

Exemplu

Intrare

 81 2 34

 64 1 50

 81 3 85

Ieșire

Explicație

Pentru a construi covorul se folosesc 3 etape de dantelare.
Fracția ce reprezintă suprafața covorului după decupare este \(\frac{3359232}{729}\)=4608
Fracția ce reprezintă perimetrul covorului după decupare \(\frac{40176}{27}\)=1488

Pentru a construi covorul se folosesc 2 etape de dantelare.
Fracția ce reprezintă suprafața covorului după decupare este \(\frac{6377472}{6400}\)=996.48
Fracția ce reprezintă perimetrul covorului după decupare \(\frac{1728}{4}\)=432

Pentru a construi covorul se folosesc 4 etape de dantelare.
Fracția ce reprezintă suprafața covorului după decupare este \(\frac{54482544}{16200}\)=
3363.12
Fracția ce reprezintă perimetrul covorului după decupare \(\frac{29856}{81}\)=7776

Cum e corect?

cout < "As la info"; cout << "As la info"; cout >> "As la info";

Felicitări! Poți mai mult?

Avem sute de probleme pentru tine, fiecare cu explicații ușor de înțeles.

Greșit, dar nu-i bai!

Antrenează-te cu sutele de probleme pe care ți le-am pregătit. Îți explicăm fiecare problemă în parte.

Rezolvare

Iată rezolvarea de 100 de puncte pentru problema Morum:

// implementare: Cristi Dospra
// punctaj: 100p
// complexitate: O( Etape * Nr Mari)

#include <fstream>
#include <vector>
#include <algorithm>
using namespace std;

#define Mod 666013

ifstream fin ( "morum.in" );
ofstream fout ( "morum.out" );

#define DigitMax 70
class Huge
{
    public: long long V[DigitMax];

    inline Huge ()
    {
        for(long long i = 0;i < DigitMax; ++i)
            V[i] = 0;
    }

    inline Huge (long long X)
    {
        *this = X;
    }

    inline Huge operator= (long long X)
    {
        for(long long i = 0;i < DigitMax; ++i)
            V[i] = 0;
        for(; X; X /= 10)
            V[++V[0]] = X % 10;
        return *this;
    }

    inline Huge operator= (Huge X)
    {
        for(long long i = 0;i < DigitMax; ++i)
            V[i] = X.V[i];
        return *this;
    }

    friend Huge operator+ (Huge V,Huge X)
    {
        long long i, T = 0;
        Huge Now;
        for(i = 1; i <= V.V[0] || i <= X.V[0] || T; i++, T /= 10)
            Now.V[i] = (T += V.V[i] + X.V[i]) % 10;
        Now.V[0] = i - 1;
        return Now;
    }
    friend Huge operator+ (Huge A,long long  X)
    {
        return A + Huge(X);
    }

    friend Huge operator* (Huge V,Huge X)
    {
        Huge Now;
        long long i, j, T = 0;
        for(i = 1; i <= V.V[0]; i ++)
        {
            for(j = 1, T = 0; j <= X.V[0] || T; j ++, T /= 10)
                Now.V[i + j - 1] = (T += Now.V[i + j - 1] + V.V[i] * X.V[j]) % 10;
            if(i + j - 2 >= Now.V[0]) Now.V[0] = i + j - 2;
        }
        return Now;
    }

    friend Huge operator* (Huge A,long long  X)
    {
        return A * Huge(X);
    }

    friend bool operator<= (Huge X,Huge Y)
    {
        long long i,n = X.V[0],m = Y.V[0];
        if(n < m)   return true;
        if(m > n)   return false;
        for(i = n; i && X.V[i] == Y.V[i]; --i);
        if(i==0)    return true;
        if(X.V[i] < Y.V[i])   return true;
        return false;
    }
    friend ostream & operator<<(ostream &out, Huge X)
    {
        for(long long i = X.V[0]; i>0; i--)
            out<<X.V[i];
        return out;
    }
};

struct Fractie{
    Huge Numarator;
    Huge Numitor;
};

vector < Huge > Power[3];

Fractie GetArea ( int L, int Model, int Etapa ){

    Fractie Arie;

    if ( Etapa == 0 ){
        for ( int i = 0; i < 3; ++i )
            Power[i].push_back(Huge(1));
    }

    if ( Model == 1 ){

        if ( Etapa > 0 ){
            Power[0].push_back( Power[0][Etapa-1] * 3LL );
            Power[1].push_back( Power[1][Etapa-1] * 4LL );
            Power[2].push_back( Power[2][Etapa-1] * 2LL );
        }

        Arie.Numarator = Power[0][Etapa] * Huge(1LL*L * L * 173LL);
        Arie.Numitor = Power[1][Etapa] * 400LL;
    }

    if ( Model == 2 ){

        if ( Etapa > 0 ){
            Power[0].push_back( Power[0][Etapa-1] * 8LL );
            Power[1].push_back( Power[1][Etapa-1] * 9LL );
            Power[2].push_back( Power[2][Etapa-1] * 3LL );
        }

        Arie.Numarator = Power[0][Etapa] * Huge(1LL*L*L);
        Arie.Numitor = Power[1][Etapa];
    }

    if ( Model == 3 ){

        if ( Etapa > 0 ){
            Power[0].push_back( Power[0][Etapa-1] * 2LL );
            Power[1].push_back( Power[1][Etapa-1] * 3LL );
        }

        Arie.Numarator = Power[0][Etapa];
        Arie.Numarator = Arie.Numarator * 3LL*173;
        Arie.Numarator = Arie.Numarator * L;
        Arie.Numarator = Arie.Numarator * L;
        Arie.Numitor = Power[1][Etapa] * 200LL;
    }

    return Arie;
}

vector < Fractie > Rec;
Fractie GetPerim( int L, int Model, int Etapa ){

    Fractie Perim;

    if ( Model == 1 ){

        Perim.Numarator = Power[0][Etapa+1] * L;
        Perim.Numitor = Power[2][Etapa];
    }

    if ( Model == 2 ){

        Fractie aux;

        aux.Numarator = Huge(4LL * L);
        aux.Numitor = Huge(1);

        Rec.push_back( aux );

        for ( int i = 1; i <= Etapa; ++i ){
            aux = Rec[i-1];
            aux.Numarator = aux.Numarator * 3;
            aux.Numarator = aux.Numarator + ( Power[0][i-1] * 4LL * L );
            aux.Numitor = Power[2][i];

            Rec.push_back(aux);
        }

        Perim = Rec.back();
    }

    if ( Model == 3 ){

        Perim.Numarator = Huge(6LL * L) * Power[0][Etapa];
        Perim.Numitor = Huge(1);
    }

    return Perim;
}

bool CmpFrac ( Fractie A, Fractie B ){

    Huge X, Y;

    X = A.Numarator * B.Numitor;
    Y = B.Numarator * A.Numitor;

    return X <= Y;
}

int main(){

    int N;
    int Model, procent;

    fin >> N >> Model >> procent;

    procent = 100 - procent;

    Fractie Arie, Perim, Limita;

    Arie = GetArea( N, Model, 0 );
    Limita.Numarator = Arie.Numarator * procent;
    Limita.Numitor = Arie.Numitor * 100LL;

    int Sol;
    for ( int Etapa = 1; ; ++Etapa ){
        Arie = GetArea( N, Model, Etapa );
        if ( CmpFrac( Arie, Limita ) ){
            Sol = Etapa-1;
            break;
        }
    }

    Arie = GetArea ( N, Model, Sol );
    Perim = GetPerim( N, Model, Sol );

    fout << Sol << "\n";
    fout << Arie.Numarator << "\n" << Arie.Numitor << "\n";
    fout << Perim.Numarator << "\n" << Perim.Numitor << "\n";

    return 0;
}

Atenție

Enunțurile afișate pe această pagină aparțin exclusiv site-ului PbInfo. Astfel, pentru ștergerea conținutului, puteți să ne contactați la adresa Adresa de email .

Rezolvarea problemei #1762 Morum

Pe această pagină găsești rezolvarea de 100 de puncte pentru problema #1762 Morum de pe PbInfo.ro. Atenție: nu încurajăm copiatul codului! Totuși, credem cu tărie că analizarea unei soluții corecte este o metodă foarte ușoară de a învăța informatică, astfel că oferim sursele pentru peste 1500 de probleme de pe platforma PbInfo.ro.

Pentru rezolvări PbInfo de la peste 1500 de probleme, vă invităm să intrați pe site-ul nostru!

Rezolvare completă PbInfo #1762 Morum