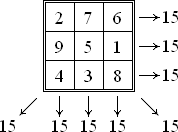
Un Pătrat Magic este un pătrat ce conține numerele de la 1 la n 2 în care sumele fiecăror linii, coloane și a celor două diagonale sunt egale. Această sumă se mai numește și constanta pătratului magic.
Cerința
Să se scrie in limbajul c++ o funcție numita magic care are ca argument un număr natural c ți care să se verifice dacă există un pătrat magic cu constanta c.
Subprogramul va returna latura pătratului, adică n, sau 0 dacă nu există pătrat magic cu constanta c.
Restricții și precizări
1 ≤ c < 18.446.744.073.709.551.616
Exemplu
magic(34) = 4, magic(88) = 0.
Cum e corect?
cout < "As la info";
cout << "As la info";
cout >> "As la info";
Felicitări! Poți mai mult?
Avem sute de probleme pentru tine, fiecare cu explicații ușor de înțeles.
Greșit, dar nu-i bai!
Antrenează-te cu sutele de probleme pe care ți le-am pregătit. Îți explicăm fiecare problemă în parte.
Rezolvare
Iată rezolvarea de 100 de puncte pentru problema PatratMagic4 :
#include <cmath>
int magic(uintmax_t c){
if(c<15) return 0;/// cel mai mic p.m. are constanta 15
/// rezolvam ec. (n*n*n + n)/2 = c, folosind ec de gr 3 redusa
/// cum avem 2 sol complexe, calculam doar cea reala
double v1 = abs(cbrt(c*1.0+sqrt(1.0/27.0+c*c*1.0)));
double v2 = abs(cbrt(c*1.0-sqrt(1.0/27.0+c*c*1.0)));
double n = v1+v2;
/// in mod mormal, avem n o valoare intreaga, dar datorita
/// impreciziei tipului double/float, rotunjim si verificam
uintmax_t rez = n;
if((rez*rez*rez+rez)/2 == c) return rez;
return 0;
}Atenție
Enunțurile afișate pe această pagină aparțin exclusiv site-ului PbInfo. Astfel, pentru ștergerea conținutului, puteți să ne contactați la adresa  .
.
Rezolvarea problemei #3332 PatratMagic4
Pe această pagină găsești rezolvarea de 100 de puncte pentru problema #3332 PatratMagic4 de pe PbInfo.ro. Atenție: nu încurajăm copiatul codului! Totuși, credem cu tărie că analizarea unei soluții corecte este o metodă foarte ușoară de a învăța informatică, astfel că oferim sursele pentru peste 1500 de probleme de pe platforma PbInfo.ro.
Pentru rezolvări PbInfo de la peste 1500 de probleme, vă invităm să intrați pe site-ul nostru!